Insiemi

Un insieme è una collezione (non ordinata) di oggetti, chiamati elementi dell’insieme.

X = { cane, patata, 3, mario }
X = { 2, 9, 7, 5, 11, ... }

A volte un insieme è determinato da una proprietà, nel senso che gli elementi che appartengono all’insieme hanno (godono) della proprietà P.

X = { x t.c. x ha la proprietà P }

per es. l’insieme dei numeri pari

X = { x t.c. x è pari } = { 2,4,6,8,... }

Una volta definita una proprietà P per un insieme X, è possibile dire se un elemento appartiene o meno all’insieme X.

E' utile introdurre due insiemi particolari, l'insieme universale U, ovvero sia l’insieme costituito da tutti gli elementi, e l'insieme nullo ∅ (o vuoto), un insieme che non contiene alcun elemento.

Un altro insieme importante è l'insieme complementare (o complemento) di X, definito come l’insieme di tutti gli elementi dell’insieme universale che non sono elementi di X,

X^c = { x ∈ U t.c x ∉ X}

Combinazioni di insiemi

Gli insiemi possono essere combinati insiemi secondo alcune regole, in particolare, dati due qualsiasi insiemi X e Y si possono definire le seguenti operazioni:

• l'unione degli insiemi X e Y è definita come l’insieme degli elementi che sono in X, Y o in entrambi, si indica come X+Y;

• l'intersezione di X e Y è l’insieme degli elementi che sono contemporaneamente in X e Y, e si indica come X ⋅ Y

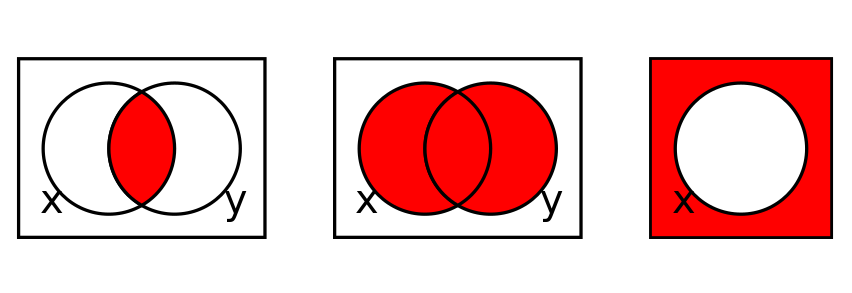
Diagrammi di Venn

Una rappresentazione utile per gli insiemi e le operazioni tra insiemi è quella dei diagrammi di Venn.
In un diagramma di Venn l’insieme dei punti racchiusi in un rettangolo è l’insieme universale. Un insieme viene rappresentato come l’insieme dei punti racchiusi da un cerchio.
Con i diagrammi di Venn è semplice visualizzare le operazioni di unione e intersezione tra insiemi e l’insieme complementare

Algebra delle proposizioni

Nell’algebra delle proposizioni si assumono come concetti primitivi quelli di proposizione, vero e falso.
Da una proposizione possiamo dedurre il significato di una frase che sia non ambigua e che abbia la proprietà di essere vera o falsa, ma non entrambe.

Da una qualsiasi proposizione p si possono formare altre proposizioni, per esempio possiamo introdurre la negazione di p, p', definita come “è falso che p”.

Due proposizioni qualsiasi p e q si possono combinare in modi diversi per ottenere una nuova proposizione.

Possiamo per esempio usare il connettivo and (congiunzione). In particolare la congiunzione di p e q è definita come la proposizione “sia p che q”, si indica con p ⋅ q e risulta essere vera solo nei casi in cui sia p che q sono vere, mentre è falsa se una delle due o entrambe sono false.

La disgiunzione di p e q, rappresentata dal connettivo or è definita come la proposizione “p oppure q”, indicata come p+q, e risulta vera se almeno una delle due proposizioni è vera, mentre è falsa se entrambe sono false.

Per completare l’algebra delle proposizioni introduciamo altre due proposizioni, rappresentate da 0 e 1. Definiamo 0 come la proposizione che è sempre falsa e 1 come quella che è sempre vera.

E' possibile costruire delle tabelle di verità per le operazioni di congiunzione (and ∧), disgiunzione (or ∨)

p	q	p ∧ q	p ∨ q
0	0	0	0
1	0	0	1
0	1	0	1
1	1	1	1

e negazione (not ¬)

p	¬ p
0	1
1	0

Algebra di Boole

L’algebra degli insiemi e l’algebra delle proposizioni sono due casi particolare di Algebra di Boole (Boolean algebra), che fu introdotta da George Boole nel 1847.
Prima di poter definire che cosa è un’algebra di Boole dobbiamo definire cosa è un’operazione binaria e alcune importanti proprietà.

Un'operazione binaria ∘ su un insieme M è una regola che assegna a una coppia ordinata (a,b) di elementi di M un unico elemento c = a ∘ b appartenente a M.

Un’operazione binaria ∘ su un insieme M è associativa se e solo se per ogni a, b e c in M,

a ∘ ( b ∘ c ) = ( a ∘ b ) ∘ c

Un’operazione binaria ∘ su un insieme M è commutativa se e solo se per ogni a e b in M,

a ∘ b = b ∘ a

Se ∘ e ∗ sono due operazioni binarie sullo stesso insieme M, ∘ è distributiva rispetto a ∘ se e solo se per ogni a, b, e c in M

a ∘ ( b ∗ c ) = ( a ∘ b ) ∗ ( a ∗ c)

Inoltre un elemento e in una classe M è un'identità per l’operazione binaria ∗ se e solo se, per ogni a in M,

a ∗ e = e ∗ a = a

Definizione di algebra di Boole

Una classe di elementi B e due operazioni binarie (+) e (∙) sono un' algebra di Boole se e solo se valgono i seguenti postulati:

1. Le operazioni (+) e (∙) sono commutative
2. In B esistono due elementi identità distinti per le operazioni (+) e (∙)
3. ciascuna (+) e (∙) è distributiva rispetto all’altra
4. per ogni a in B esiste un elemento a' in B tale che
   

   a + a' = 1, a (∙) a' = 0

Le due operazioni binarie possono essere indicate in qualsiasi modo, al posto di (+) e (∙) potremmo usarealtri simboli, per esempio ∗ e ∘, oppure ∪ e ∩.

L’algebra degli insiemi e l’algebra delle proposizioni soddisfano le proprietà 1-4 e sono dunque esempi di algebre di Boole

Un caso molto importante di algebra di Boole è quella che opera su una classe con soli due elementi, 0 e 1.

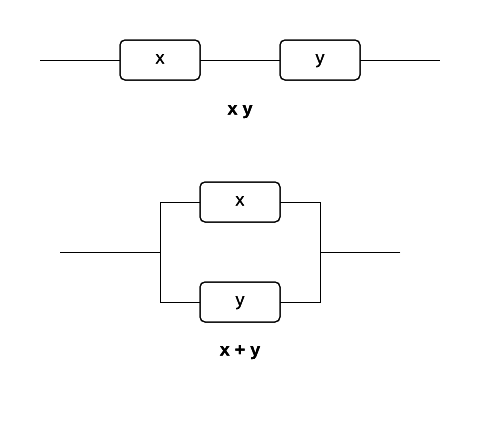
Algebra dei circuiti

Consideriamo adesso i circuiti elettrici che siano composti da dispositivi che abbiano due soli stati logici, per esempio acceso, spento, oppure chiuso, aperto.

All’inizio del XX secolo alcuni ingegneri elettronici osservarono che il comportamento di alcuni componenti elettronici era analogo a quello descritto da un’algebra di Boole costituita da solo due elementi, 0 e 1.

Questo significa che il comportamento di questi circuiti è identico a quello già descritto per l’algebra delle preposizioni.

Il contributo teorico fondamentale per l’algebra dei circuiti fu formulato nel 1937 nella sua tesi di laurea da Claude Shannon, padre della teoria dell’informazione.

Circuiti per il calcolo aritmetico

Sistema di numerazione binario

Un numero N è un simbolo costituito da una sequenza di k+1 cifre,

N = a_kR^k + ...+ a₂R² + a₁R¹ + a₀R⁰

dove R è la radice del sistema di numerazione e può essere un qualsiasi numero intero, e dove i coefficienti

a_k , ... , a₂ , a₁ , a₀

sono delle cifre minori del valore della radice scelta.

Se consideriamo R=2 allora abbiamo solo due cifre per rappresentare i coefficienti, 0 e 1. Un numero così fatto può essere rappresentato da una sequenza di interruttori, luci, relé etc, ciascuno dei quali abbia due soli stati corrispondenti a 0 e 1.
Questo sistema si chiama sistema dei numeri binari.